Historia de las matemáticas

3000 A.C.- 2500 A.C.	Los textos de matemática más antiguos que se poseen proceden de Mesopotamia, algunos textos cuneiformes tienen más de 5000 años de edad. Se inventa en China el ábaco, primer instrumento mecánico para calcular. Se inventan las tablas de multiplicar y se desarrolla el cálculo de áreas.
1600 A.C  aprox.	El Papiro de Rhind, es el principal texto matemático egipcio, fué escrito por un escriba bajo el reinado del rey hicso Ekenenre Apopi  y contiene lo esencial del saber matemático de los egipcios. Entre estos, proporciona unas reglas para cálculos de adiciones y sustracciones de fracciones, ecuaciones simples de primer grado, diversos problemas de aritmética, mediciones de superficies y volumenes.
entre 600 y 300 A.C.	La matemática griega es conocida gracias a un prólogo histórico escrito en el siglo V D.C. por el filósofo Proclo. Este texto nombra a los geómetras griegos de aquel período, pero sin precisar la naturaleza exacta de sus descubrimientos.
Del 550 al 450 A.C.	Se establece la era pitagórica. Pitágoras de Samos, personaje semilegendario creador de un gran movimiento metafísico, moral, religioso y científico. El saber geométrico de los pitagóricos estaba en la geometría elemental, donde destaca el famoso Teorema de Pitágoras, el cual fue establecido por su escuela y donde la tradición de los pitagóricos llevó a atribuirselo a su maestro. Con respecto a la aritmética el saber de los pitagóricos era enorme. Fueron los primeros en analizar la noción de número y en establecer las relaciones de correspondencia entre la aritmética y la geometría. Definieron los número primos, algunas progresiones y precisaron la teoría de las proporciones. Los pitagóricos propagaban de que todo podía expresarse por medio de números, pero luego tuvieron que aceptar que la diagonal de un cuadrado era inconmesurable con el lado del cuadrado.
Hacia el 460 A.C	El mercader Hipócrates de Quíos, se convirtió en el primero en redactar unos Elementos, es decir, un tratado sistemático de matemáticas.
alrededor de 406 a 315 A.C.	El astrónomo Eudoxo, establece una Teoría de la Semejanza.
276-194 A.C.	El matemático griego Eratóstenes ideó un método con el cual pudo medir la longitud de la circunferencia de la tierra.
300-600	Los hindúes conocen el sistema de numeración babilónica por posición y lo adaptan a la numeración decimal, creando así el sistema decimal de posición, que es nuestro sistema actual.
1100	Omar Khayyam desarrolla un método para dibujar un segmento cuya longitud fuera una raíz real positiva de un polinomio cúbico dado.
1525	El matemático alemán Christoff Rudolff emplea el símbolo actual de la raíz cuadrada
1545	Gerolamo Cardano publica el método general para resolver ecuaciones de tercer grado
1550	Ferrari da a conocer el método general de resolución de una ecuación de cuarto grado
1591	Francois Viète escribió In artem analyticem isagoge en el cual se aplicaba por primera vez el álgebra a la geometría.
1614	Napier inventa los logaritmos.
1617	John Napier inventa un juego de tablas de multiplicación, llamada "los huesos de Napier". Posteriormente publicó la primera tabla de logaritmos.
1619	Descartes crea la Geometría Analítica.
1642	El matemático Blaise Pascal construye la primera máquina de calcular, conocida como la Pascalina, la cual podía efectuar sumas y restas de hasta 6 cifras.
1684	Se crea, casi simultáneamente, el Cálculo Infinitesimal por Newton y Leibniz.
1743	Langlois inventa el pantógrafo.
1746	D'Alembert enuncia y demuestra parcialmente que "cualquier polinomio de grado n, tiene n raíces reales o complejas".
1761	Johann Lambert prueba que el número p es irracional.
1777	Leonard Euler   matemático suizo, simboliza la raíz cuadrada de -1 con la letra i (de imaginario).
1798	El matemático italiano Paolo Ruffini  enuncia y parcialmente demuestra  la imposibilidad de resolver ecuaciones de 5º grado.
1812	Laplace publicó en París su Théorie analytique des probabilités donde hace un desarrollo riguroso de la teoría de la probabilidad con aplicaciones a problemas demográficos, jurídicos y explicando diversos hechos astronómicos.
1817	Bernhard Bolzano presenta un trabajo titulado "Una prueba puramente analítica del teorema que establece que entre dos valores donde se garantice un resultado opuesto, hay una raíz real de la ecuación". Dicha prueba analítica se conoce hoy como teorema de Bolzano
1822	Poncelet descubre lo que él llamó "Propiedades Proyectivas de las Figuras"
1831	G.W.Leibniz  pone de manifiesto el valor del concepto de grupo, abriendo la puerta a las más importantes ideas matemáticas del mundo contemporáneo.
1872-1895	Es creada la Teoría de Conjuntos por el matemático ruso Georg Cantor.
1904	El matemático sueco Niels F. Helge von Koch  construye la curva que lleva su nombre.
1924	Se instauran las medallas fields con el fin de premiar a matemáticos destacados.
1975	Mitchell Feingenbaum descubre un modelo matemático que describe la transición del orden al caos.
1977	Los matemáticos K. Appel y W. Haken resuelven el histórico teorema de los cuatro colores con ayuda de un computador.

Lectura y escritura de decimales

Partes de los decimales

Los decimales son fracciones con denominadores especiales.

Se escriben como décimas, centésimas y milésimas, dado que el valor posicional de los decimales indica el valor de cada dígito.  

A diferencia de los números enteros, los decimales poseen valores posicionales a la derecha del punto o coma decimal.

Número decimal: Décimas, centésimas y milésimas.

El punto o coma decimal también se puede leer como “punto” o “coma” y los dígitos se pueden leer de forma separada.

Números decimales: Unidades 1/1. Décimos 1/10. Centésimos 1/100. Milésimos. 1/1000.

Por ejemplo, tienes 15 dólares y 25 centavos, esto se escribe como US$ 15.25 se lee como: quince dólares y veinticinco centavos, también se puede decir quince punto veinticinco.

Las fracciones en forma de decimales

Como ya dijimos, los números decimales son otra forma de representar las fracciones, por esto, algunas fracciones se pueden convertir en números decimales.

Por ejemplo:

8/10 (ocho décimos) es lo mismo que 8 dividido 10 y el resultado de esto es: 0.8 (0,8) y se lee cero punto ocho.

¿las fracciones?

¿Sabes para qué sirven las fracciones, qué significan y cómo pueden entenderse? Muchas veces nos encontramos con operaciones de números fraccionarios, pero no entendemos qué significan o qué quieren decir. Con esta infografía despejarás esas inquietudes.

partes de una división

Dividendo: 

Es el número que se ha de dividirse o repartirse en grupos o partes.

Residuo: 

Se refiere a los restos. Es lo que sobra del dividendo después de haberlo fragmentado en grupos iguales. 

Divisor: 

Corresponde al número de grupos iguales en los que se ha de fragmentar al dividendo.

Cociente: 

Es el resultado de la división. Es la cantidad que le corresponde a cada uno de los grupos en los que se fragmentó al dividendo.

¿Como dividir? ¿Qué pasa cuando dividimos?

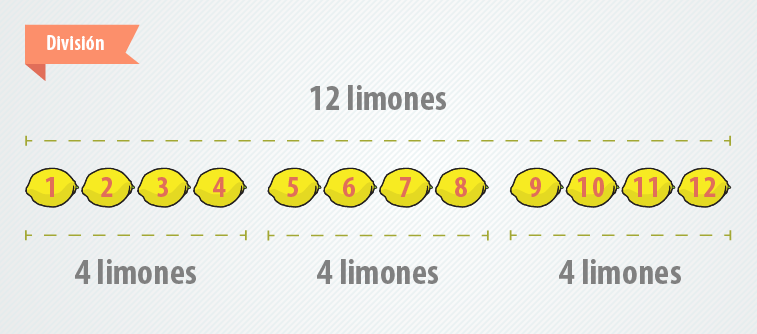
Supongamos que tienes 12 limones y quieres repartirlos entre 3 miembros de tu familia. Si distribuyes los limones equitativamente, ¿cuántos limones recibirá cada persona?

Para averiguarlo, tenemos que hacer una división que lucirá así expresada de forma matemática: 12 ÷ 3 = ?

Repartir 12 limones en 3 grupos de 4 limones cada uno.

La respuesta es 3, debido a que con 12 limones podemos formar 3 grupos de 4 limones cada uno y así repartir de forma equitativa entre los miembros de tu familia.

De esta forma, podemos ver que 12 ÷ 3 = 4. Esto también se puede escribir asi: 12 / 3 = 4. La barra oblicua ( / ), significa dividido entre.

Ubicación de los números en la división

Si se trata de dividir números pequeños, los puedes escribir en la misma línea con el signo barra ( / ) en el medio, así: 6 / 3 = ?.

Si se trata de dividir números grandes, te aconsejamos ubicarlos en columnas.

La Importancia de las Matemáticas en la Vida (VIDEO)

aquí tenemos un vídeo acerca de como las matemáticas afectan nuestra vida.
recomendado!!

La Importancia De La Matematica En La Vida

Las matemáticas son fundamentales para el desarrollo intelectual de los niños, les ayuda a ser lógicos, a razonar ordenadamente y a tener una mente preparada para el pensamiento, la crítica y la abstracción.

Las matemáticas configuran actitudes y valores en los alumnos pues garantizan una solidez en sus fundamentos, seguridad en los procedimientos y confianza en los resultados obtenidos. Todo esto crea en los niños una disposición consciente y favorable para emprender acciones que conducen a la solución de los problemas a los que se enfrentan cada día.

A su vez,  las matemáticas contribuyen a la formación de valores en los niños, determinando sus actitudes y su conducta, y sirviendo como patrones para guiar su vida, como son, un estilo de enfrentarse a la realidad lógico y coherente, la búsqueda de la exactitud en los resultados, una comprensión y expresión clara a través de la utilización de símbolos, capacidad de abstracción, razonamiento y generalización y la percepción de la creatividad como un valor.

Podemos dividir estos valores en dos grupos:

1) Valores de la inteligencia: afán de saber, adquirir conocimientos, estudiar, hábitos y técnicas de trabajo intelectual para utilizar la información, sentido crítico de lo verdadero;

2) Valores de la voluntad: a) Capacidad de decisión (prudencia, predicción, iniciativa, seguridad, confianza en sí mismo), b) Valores morales: respecto a las creencias e ideas de los demás, colaboración, solidaridad, honradez, honestidad, laboriosidad, optimismo.

Sin embargo en el colegio, la asignatura de matemáticas suele ser de lejos, la más odiada. Y ¿Por qué? Parece que nos estamos dando cuenta de que las matemáticas llevan años enseñándose mal. Es necesario que desde la escuela se transmita una idea positiva de las matemáticas y para ello hay que cambiar la manera en la que se les presentan a los alumnos.

En este vídeo realizado por el Banco Interamericano de Desarrollo (BID) hacen algunas propuestas.

El éxito en la vida comienza por el éxito en las matemáticas.